Correlation and Causation

Correlation measures the degree to which two phenomena are related to one another. For example, there is a correlation between summer temperatures and ice cream sales. When one goes up, so does the other. Two variables are said to be

1. Positively correlated – When a change in one is associated with the change in another in the same direction.
2. Negatively correlated – When a change in one is associated with the change in another in the opposite direction.
3. Zero correlation – If the two variables have no association with one another.

Some examples

1. Positively correlated   – Height and Weight are positively correlated. Taller people weigh more than the shorter people on average.
2. Negatively correlated  – Body weight and Exercise. On average you will weigh more if you do not exercise and  less otherwise.
3. Zero correlation – Your hip size and SAT score.

Scatter Plots

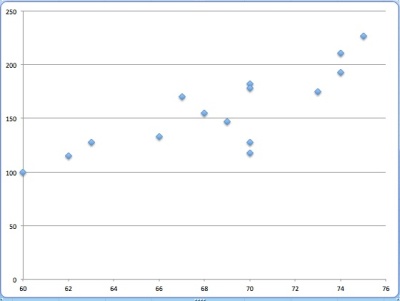
Scatter plots can be used for finding out the correlation between 2 variables. Given below are the data for height and weight.

Height (inches)	Weight(pounds)
74	193
66	133
68	155
69	147
73	175
70	128
60	100
63	128
67	170
70	182
70	178
70	118
75	227
62	115
74	211

Scatter plot with height on X axis and weight on Y axis

From the chart you can clearly see they are positively correlated. This works well on smaller dataset. If you need to analyze lots of data then it is not easy to interpret the results from the scatter plot. What we need is a descriptive statistic which summarizes huge quantities of data into a single number. Correlation coefficient is used for this purpose.

Correlation Coefficient

Correlation coefficient is a single number ranging from -1 to +1.

A correlation of 1 between two variables indicates that the change in one variable will result in equivalent change in the other variable in the same direction.

A correlation of -1 indicates that the change in one variable results in a equivalent change in other variable in the opposite direction.

A correlation of 0 indicates that there is no relation between the two variables.

How to calculate correlation coefficient

I am taking this example from the book Naked Statistics. Using the same height and weight example, let us calculate the correlation coefficient.

Height (inches)	Weight (pounds)	A	B	A * B
74	193	1.21	0.99	1.19
66	133	(0.63)	(0.67)	0.42
68	155	(0.17)	(0.06)	0.01
69	147	0.06	(0.29)	(0.02)
73	175	0.98	0.49	0.48
70	128	0.29	(0.81)	(0.24)
60	100	(2.00)	(1.59)	3.18
63	128	(1.31)	(0.81)	1.07
67	170	(0.40)	0.35	(0.14)
70	182	0.29	0.68	0.20
70	178	0.29	0.57	0.17
70	118	0.29	(1.09)	(0.32)
75	227	1.44	1.93	2.77
62	115	(1.54)	(1.17)	1.81
74	211	1.21	1.49	1.79

1. Find out the standard deviation for both height and weight. To learn about standard deviation refer to the post here. You will get 4.36 and 36.12 as the standard deviation for height and weight.
2. Find out the mean for both height and weight. To learn about mean refer to the post here. You will get the mean height and weight as 68.73 and 157.33.
3. To calculate the values for the 3rd column as indicated by A (Height in standard units) you need to do (height – mean height) / standard deviation for height. For the first entry this comes to (74 – 68.73) / 4.36 = 1.21
4. To calculate the values for the 4th column as indicated by B (Weight in standard units) you need to do (weight – mean height) / standard deviation for weight. For the first entry this comes to (193 – 157.33) / 36.12 = 0.99
5. Calculate the product of A and B and put in column 5 as indicated by A * B. Think why did we multiply?
6. Take the average of column A * B and you get the correlation coefficient. This will come to 0.83 which is the correlation coefficient

The value of 0.83 indicates that height and weight are positively correlated. Do not worry if you do not get the math. As long as you understand what the value means you should be good. There are tools available to do the math.

How does Netflix recommends movies

In the book Naked Statistics the author writes

At the most basic level, Netflix is exploiting the concept of correlation. First, I rate a set of films. Netflix compares my ratings with those of other customers to identify those whose ratings are highly correlated with mine. Those customers tend to like the films that I like.  Once that is established, Netflix can recommend films that like-minded customers have rated highly but that I have not seen. That’s the big picture. The actual methodology is much more complex.

Causation

Strong correlation between two variables does not mean that the change in one variable is causing the change in other. Let me give an example taken from the book The Halo Effect.

A famous statistician once showed a precise correlation between arrests for public drunkenness and the number of Baptist preachers in nineteenth-century America. The correlation is real and intense, but we may assume that the two increases are causally unrelated, and that both arise as consequences of a single different factor: a marked general increase in the American population.

This is an important concept and we confuse correlation and causation a lot in our life. In the book Thinking Statistically the author writes

A classic example of “correlation does not imply causation” is the famous story that ice-cream sales over the course of a year tend to correlate with the number of drownings. Does this mean that, say, eating ice-cream causes significant groups of children to go sugar-crazy and fall in a lake? Or, even more bizarrely, that while people are drowning they suddenly consume a lot of ice-cream? Well, unsurprisingly, no. ice-cream sales tend to go up in summer, a time when people also spend more time swimming outdoors, so rising ice-cream sales and increased drownings are both caused by warmer weather but aren’t related directly.

If you think this is silly and no one would make such a basic causation-and-correlation mistake.

Public health experts in the 1940s noticed a correlation between polio cases and ice-cream consumption; they recommended cutting out ice-cream to protect against the disease. It later turned out that, you guessed it, polio outbreaks were more common in summer, and ice-cream eating was more common in summer, and polio and ice-cream had nothing to do with each other.

If you ask the CEO the following question. What is the secret of your company’s high performance. One of the answers we often hear is our employees are happy and hence there is a low employee turnover which caused the success. Is that a correlation or causation? Excerpt from the book The Halo Effect

Now the challenge is to untangle the direction of causality. Does lower employee turnover lead to higher company performance? Perhaps, since a company with a stable workforce might be able to provide more dependable customer service, spend less on hiring and training and so forth. Or does higher company performance lead to lower employee turnover? That could be true as well, since a profitable and growing company might offer a more stimulating and rewarding environment as well as greater opportunities for advancement. Knowing which leads to which is critical.

Closing Thoughts

A correlation by itself does not explain anything. If you ask people who made a lot of money they will tell that it is their skill and hard work that made money for them.

My Skill = Money I made

But the statement misses out one key variable which is serendipity. If you look around there are people with much more skills who have not made any money at all.

My Skill + Serendipity = Money I made

Appreciating the role of serendipity will help us to be better persons without ego. One who does not understand this is confusing correlation as causation.