Tf-Idf and Cosine similarity

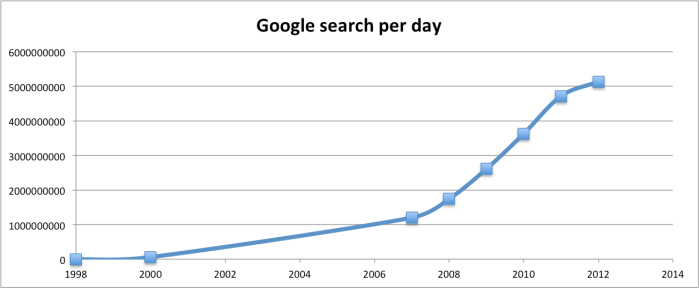
In the year 1998 Google handled 9800 average search queries every day. In 2012 this number shot up to 5.13 billion average searches per day. The graph given below shows this astronomical growth.

Year	Average Search per day
1998	9800
2000	60000000
2007	1200000000
2008	1745000000
2009	2610000000
2010	3627000000
2011	4717000000
2012	5134000000

The major reason for google’s success is because of its pageRank algorithm. PageRank determines how trustworthy and reputable a given website is. But there is also another part. The input query entered by the user should be used to match the relevant documents and score them. In this post I will focus on the second part. I have created 3 documents to show how this works. Take some time to go through them.

Document 1: The game of life is a game of everlasting learning
Document 2: The unexamined life is not worth living
Document 3: Never stop learning

Let us imagine that you are doing a search on these documents with the following query: life learning

The query is a free text query. It means a query in which the terms of the query are typed freeform into the search interface, without any connecting search operators.

Let us go over each step in detail to see how it all works.

Step 1: Term Frequency (TF)

Term Frequency also known as TF measures the number of times a term (word) occurs in a document. Given below are the terms and their frequency on each of the document.

TF for Document 1

Document1	the	game	of	life	is	a	everlasting	learning
Term Frequency	1	2	2	1	1	1	1	1

TF for Document 2

Document2	the	unexamined	life	is	not	worth	living
Term Frequency	1	1	1	1	1	1	1

TF for Document 3

Document3	never	stop	learning
Term Frequency	1	1	1

In reality each document will be of different size. On a large document the frequency of the terms will be much higher than the smaller ones. Hence we need to normalize the document based on its size. A simple trick is to divide the term frequency by the total number of terms. For example in Document 1 the term game occurs two times. The total number of terms in the document is 10. Hence the normalized term frequency is 2 / 10 = 0.2. Given below are the normalized term frequency for all the documents.

Normalized TF for Document 1

Document1	the	game	of	life	is	a	everlasting	learning
Normalized TF	0.1	0.2	0.2	0.1	0.1	0.1	0.1	0.1

Normalized TF for Document 2

Document2	the	unexamined	life	is	not	worth	living
Normalized TF	0.142857	0.142857	0.142857	0.142857	0.142857	0.142857	0.142857

Normalized TF for Document 3

Document3	never	stop	learning
Normalized TF	0.333333	0.333333	0.333333

Given below is the code in python which will do the normalized TF calculation.

def termFrequency(term, document):
	normalizeDocument = document.lower().split()
	return normalizeDocument.count(term.lower()) / float(len(normalizeDocument))

Step 2: Inverse Document Frequency (IDF)

The main purpose of doing a search is to find out relevant documents matching the query. In the first step all terms are considered equally important. In fact certain terms that occur too frequently have little power in determining the relevance. We need a way to weigh down the effects of too frequently occurring terms. Also the terms that occur less in the document can be more relevant. We need a way to weigh up the effects of less frequently occurring terms. Logarithms helps us to solve this problem.

Let us compute IDF for the term game

IDF(game) = 1 + loge(Total Number Of Documents / Number Of Documents with term game in it)

There are 3 documents in all = Document1, Document2, Document3
The term game appears in Document1

IDF(game) = 1 + loge(3 / 1)
          = 1 + 1.098726209
          = 2.098726209

Given below is the IDF for terms occurring in all the documents. Since the terms: the, life, is, learning occurs in 2 out of 3 documents they have a lower score compared to the other terms that appear in only one document.

Terms	IDF
the	1.405507153
game	2.098726209
of	2.098726209
life	1.405507153
is	1.405507153
a	2.098726209
everlasting	2.098726209
learning	1.405507153
unexamined	2.098726209
not	2.098726209
worth	2.098726209
living	2.098726209
never	2.098726209
stop	2.098726209

Given below is the python code to calculate IDF

def inverseDocumentFrequency(term, allDocuments):
	numDocumentsWithThisTerm = 0
	for doc in allDocuments:
		if term.lower() in allDocuments[doc].lower().split():
			numDocumentsWithThisTerm = numDocumentsWithThisTerm + 1

	if numDocumentsWithThisTerm > 0:
		return 1.0 + log(float(len(allDocuments)) / numDocumentsWithThisTerm)
	else:
		return 1.0

Step 3: TF * IDF

Remember we are trying to find out relevant documents for the query: life learning

For each term in the query multiply its normalized term frequency with its IDF on each document. In Document1 for the term life the normalized term frequency is 0.1 and its IDF is 1.405507153. Multiplying them together we get 0.140550715 (0.1 * 1.405507153). Given below is TF * IDF calculations for life and learning in all the documents.

	Document1	Document2	Document3
life	0.140550715	0.200786736	0
learning	0.140550715	0	0.468502384

Step 4: Vector Space Model – Cosine Similarity

From each document we derive a vector. If you need some refresher on vector refer here. The set of documents in a collection then is viewed as a set of vectors in a vector space. Each term will have its own axis. Using the formula given below we can find out the similarity between any two documents.

Cosine Similarity (d1, d2) =  Dot product(d1, d2) / ||d1|| * ||d2||

Dot product (d1,d2) = d1[0] * d2[0] + d1[1] * d2[1] * … * d1[n] * d2[n]
||d1|| = square root(d1[0]2 + d1[1]2 + ... + d1[n]2)
||d2|| = square root(d2[0]2 + d2[1]2 + ... + d2[n]2)

Vectors deals only with numbers. In this example we are dealing with text documents. This was the reason why we used TF and IDF to convert text into numbers so that it can be represented by a vector.

Refer to the link for detailed explanation of cosine similarity and vector space model. I found the following explanation in the book Mahout in Action very useful.

The cosine measure similarity is another similarity metric that depends on envisioning user preferences as points in space.  Hold in mind the image of user preferences as points in an n-dimensional space. Now imagine two lines from the origin, or  point (0,0,…,0), to each of these two points. When two users are similar, they’ll have similar ratings, and so will be  relatively close in space—at least, they’ll be in roughly the same direction from the origin. The angle formed between these two lines will be relatively small. In contrast, when the two users are dissimilar, their points will be distant, and likely in different directions from the origin, forming a wide angle. This angle can be used as the basis for a similarity metric in the same way that the Euclidean distance was used to form a similarity metric. In this case, the cosine of the angle leads to a similarity value. If you’re rusty on trigonometry, all you need to remember to understand this is that the cosine value is always between –1 and 1: the cosine of a small angle is near 1, and the cosine of a large angle near 180 degrees is close to –1. This is good, because small angles should map to high similarity, near 1, and large angles should map to near –1.

The query entered by the user can also be represented as a vector. We will calculate the TF*IDF for the query

	TF	IDF	TF*IDF
life	0.5	1.405507153	0.702753576
learning	0.5	1.405507153	0.702753576

Let us now calculate the cosine similarity of the query and Document1. You can do the calculation using this tool.

Cosine Similarity(Query,Document1) = Dot product(Query, Document1) / ||Query|| * ||Document1||

Dot product(Query, Document1) 
     = ((0.702753576) * (0.140550715) + (0.702753576)*(0.140550715))
     = 0.197545035151

||Query|| = sqrt((0.702753576)2 + (0.702753576)2) = 0.993843638185

||Document1|| = sqrt((0.140550715)2 + (0.140550715)2) = 0.198768727354

Cosine Similarity(Query, Document) = 0.197545035151 / (0.993843638185) * (0.198768727354)
                                        = 0.197545035151 / 0.197545035151
                                        = 1

Given below is the similarity scores for all the documents and the query

	Document1	Document2	Document3
Cosine Similarity	1	0.707106781	0.707106781

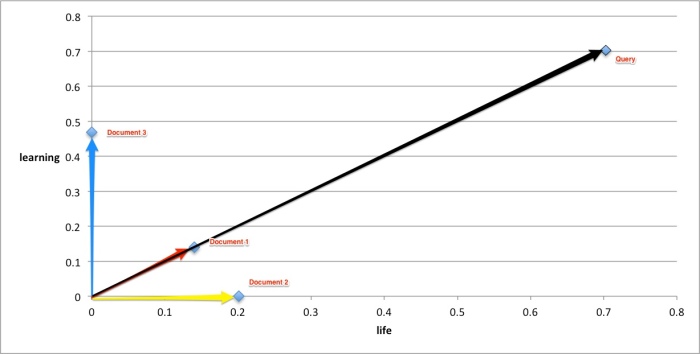
I plotted vector values for the query and documents in 2-dimensional space of life and learning. Document1 has the highest score of 1. This is not surprising as it has both the terms life and learning.